TEK 1/2022 -lehdessä julkaistujen Pulmien ja Sudokun ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen ja Esa Vesalainen, Sudoku: Arto Inkala
PULMA 1
Ongelma: Kymmenen ystävystä päättää pelata koripallo-ottelun viisi vastaan viisi. Ystävysten joukkoon kuuluu kaksi sisarusparvea, kummassakin kolme sisarusta, jotka haluavat keskenään samaan joukkueeseen. Miten monella tavalla joukkuejako voidaan tehdä (pelipaikoilla ei ole väliä)?
Ratkaisu: Sisarusparvien on oltava keskenään eri joukkueissa. Tarkastellaan nyt miten monella tavalla loput kaksi pelaajaa voidaan valita toiseen joukkueeseen. Jäljellä on neljä pelaajaa, näistä voidaan valita kaksi kuudella tavalla, kun järjestyksellä tai pelipaikalla ei ole väliä. Vaihtoehtoja on siis yhteensä kuusi.
PULMA 2
Ongelma: Mitkä luvuista 1, 11, 111, 1111, 11111, 111111, ... ovat jaollisia seitsemällä?
Ratkaisu: On helppo tarkistaa, että luvut 1, 11, 111, 1111 ja 11111 ovat seitsemällä jaottomia, kun taas 111111 on seitsemällä jaollinen. Jos numeroita on enemmän kuin kuusi, niin niitä on 6k+r kappaletta, missä k on positiivinen kokonaisluku ja r on jokin luvuista 1, 2, 3, 4, 5 ja 6. Tällöin
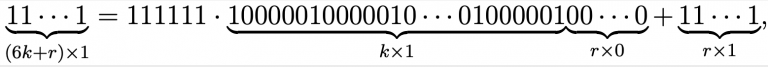
missä oikealla puolella ensimmäinen termi on jaollinen seitsemällä, joten koko oikea puoli on jaollinen seitsemällä täsmälleen silloin kun r=6. Täten luku 11...1 on jaollinen seitsemällä täsmälleen silloin kun numeroita on kuudella jaollinen määrä.
PULMA 3
Ongelma: Eräänä kauniina kesäpäivänä eräälle 8x8-ruudukolle muuttaa asumaan sieniyhteisö. Jokaisena aamuna tietyssä ruudussa on sieni täsmälleen silloin, kun jossakin kyseisen ruudun naapuriruudussa oli sieni edellisenä päivänä. (Kaksi eri ruutua ovat naapuriruutuja silloin, kun niillä on yhteinen sivu.) Missä ruuduissa sienet voivat sijaita ensimmäisenä kauniina kesäpäivänä, jos jonakin päivänä jokaisessa ruudussa on sieni?
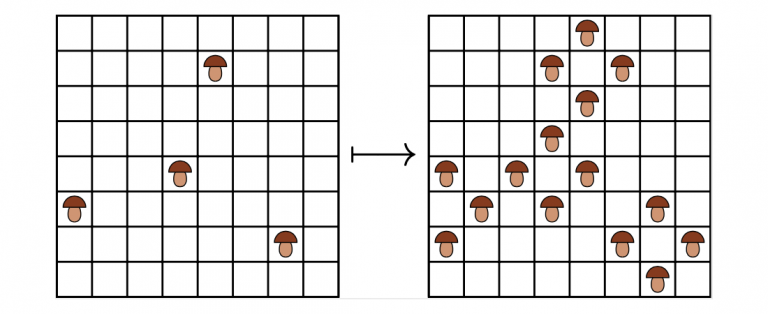
Ratkaisu: Värittäkäämme ruudut mustalla ja valkealla kuten shakkilauta:

Jos ensimmäisenä kesäpäivänä sieniä on vain mustissa ruuduissa, niin silloin sieniä on seuraavana päivänä vain valkeissa ruuduissa, sitä seuraavana päivänä vain mustissa ruuduissa, ja niin edelleen. Erityisesti, silloin enintään puolessa ruuduista voi koskaan olla sieniä. Samoin käy, jos ensimmäisenä kesäpäivänä sieniä oli vain valkeissa ruuduissa. Jos sienet onnistuvat lopulta valloittamaan kaikki ruudut, oli ensimmäisenä kesäpäivänä oltava ainakin yksi sieni mustassa ruudussa ja ainakin yksi sieni valkeassa ruudussa.
Seuraavaksi toteamme, että jos alussa yhdessä, vaikkapa valkeassa, ruudussa on sieni, niin kahden päivän kuluttua tässä ruudussa ja kahden ruudun päässä olevissa valkeissa ruuduissa on sieniä, neljän päivän kuluttua tämä valkeissa ruuduissa olevien sienten joukkio on kasvanut kaikkiin enintään neljän ruudun päässä oleviin valkeisiin ruutuihin, ja lopulta kaikissa valkeissa ruuduissa on oltava sieni:

Samoin käy, jos alussa ainakin yhdessä mustassa ruudussa on sieni.
Lopuksi, koska sienten lisääminen tyhjiin ruutuihin ei voi pienentää seuraavan päivän sieniruutujen joukkoa, toteamme, että sienet peittävät lopulta koko ruudukon täsmälleen silloin, kun ensimmäisenä kesäpäivänä sieniä oli ainakin yhdessä valkeassa ruudussa ja ainakin yhdessä mustassa ruudussa.
PULMA 4
Ongelma: Olkoot AC ja BD ympyrän kaksi eri halkaisijaa. Piste P sijaitsee ympyrällä niin, että AP=a, BP=b ja CP=c. Kuinka pitkä on silloin DP?
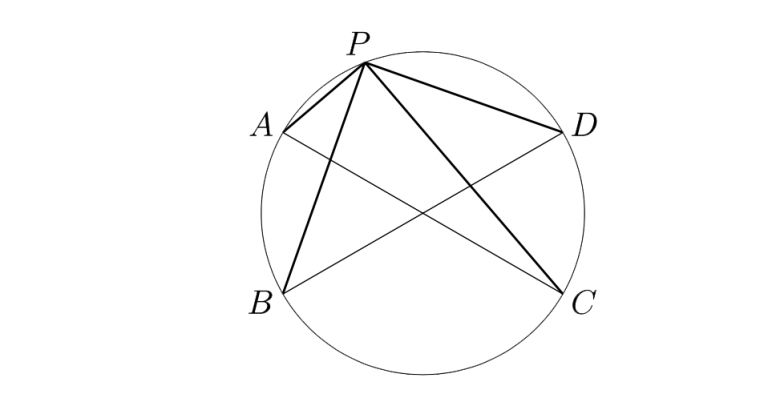
Ratkaisu: Merkitkäämme d=DP. Puoliympyrän kaarta vastaava kehäkulma on aina suora, joten kolmiot PAC ja PBD ovat suorakulmaisia kolmioita, joiden hypotenuusat ovat ympyrän halkaisijat AC ja BD. Pythagoraan lauseen nojalla silloin a^2+c^2=AC^2 ja b^2+d^2=BD^2. Koska ympyrän halkaisijat ovat keskenään yhtä pitkiä, on AC=BD. Siispä a^2+c^2=b^2+d^2, mistä voimme ratkaista
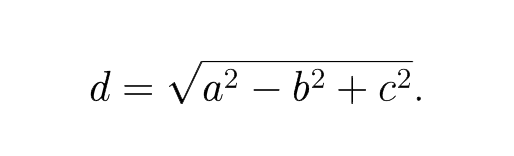

Tehtävät laatineet: Anne-Maria Ernvall-Hytönen, Esa Vesalainen. Sudoku: Arto Inkala
TEK 5/2021 -lehdessä julkaistujen Pulmien ja Sudokun ratkaisut:
PULMA 1.
Ongelma.
Jos kaikki söpöt eläimet ovat pörröisiä, kaikki vihreät eläimet ovat söpöjä, kaikki pienet eläimet ovat söpöjä ja kaikki söpöt, pörröiset eläimet ovat vihreitä, niin mikä seuraavista väitteistä ei välttämättä ole tosi?
a) Kaikki pienet eläimet ovat pörröisiä.
b) Kaikki söpöt eläimet ovat vihreitä.
c) Kaikki pörröiset eläimet ovat vihreitä.
d) Kaikki pienet eläimet ovat vihreitä.
e) Kaikki pienet, vihreät eläimet ovat pörröisiä.
Ratkaisu. Väite c) ei välttämättä ole tosi. Osoitetaan ensin, että se ei välttämättä ole tosi ja osoitetaan sitten, että kaikki muut väitteet ovat välttämättä tosia.
Tarkastellaan kahden eläimen joukkoa. Toinen eläin on pieni, söpö, vihreä ja pörröinen. Toinen eläin on suuri, sininen, epäsöpö ja pörröinen. Tämä joukko toteuttaa annetut ehdot, mutta ei kohdan c) väittämää.
Väite a) sen sijaan on välttämättä tosi, koska kaikki pienet eläimet ovat söpöjä, ja kaikki söpöt eläimet pörröisiä.
Väite b) on tosi, koska kaikki söpöt eläimet ovat pörröisiä, ja kaikki söpöt, pörröiset eläimet vihreitä.
Väite d) on tosi, koska kaikki pienet eläimet ovat söpöjä, kaikki söpöt pörröisiä ja kaikki söpöt, pörröiset eläimet vihreitä.
Väite e) on tosi, koska kaikki pienet eläimet ovat söpöjä ja kaikki söpöt pörröisiä, jolloin erityisesti kaikki vihreät pienet eläimet ovat pörröisiä.
PULMA 2.
Ongelma.
Kuinka suuri on summa
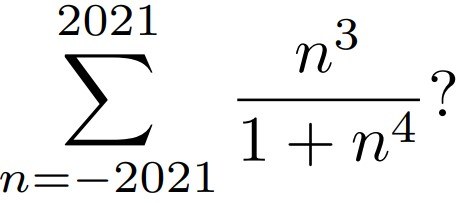
Ratkaisu.
Koska jokaisella kokonaisluvulla n on
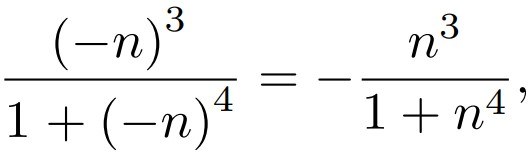
supistuvat summassa ensimmäinen ja viimeinen termi pois, samoin toinen ja toiseksi viimeinen termi pois, ja niin edelleen, kunnes jäljelle jää vain keskimmäinen termi, joka vastaa indeksin n arvoa n=0. Mutta tämä viimeinen termi on luonnollisesti nollan suuruinen. Täten summan arvo on 0.
PULMA 3.
Ongelma.
Mikä on lukujen
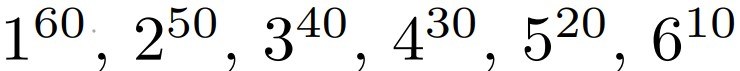
keskinäinen suuruusjärjestys?
Ratkaisu.
Osoitamme, että lukujen keskinäinen suuruusjärjestys on 1^60<6^10<5^20<2^50<4^30<3^40.
Todetaan aluksi, että luku 1^60=1 on pienin, koska muut luvut ovat varmasti isompia kuin 1. Todetaan seuraavaksi, että 6^10<5^20, onhan nimittäin
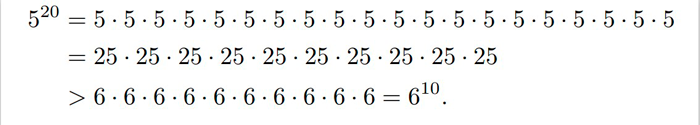
Täysin samassa hengessä voimme todeta, että
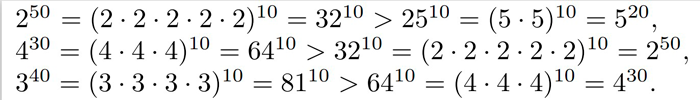
Ongelma.
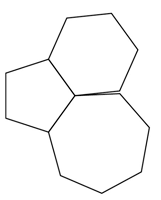
Seuraavassa kuvassa on säännöllinen viisikulmio, jolla on yhteinen sivu säännöllisen kuusikulmion kanssa, ja toinen yhteinen sivu säännöllisen seitsenkulmion kanssa. Kuinka suuri kulma syntyy kuusikulmion ja seitsenkulmion väliin?
Ratkaisu.
Olkoon n kokonaisluku, joka on vähintään 3. Kun säännöllinen n-kulmio pilkotaan n-2 kolmioksi, nähdään, että sen kulmien summan on oltava kolmioiden kulmien summien summa, eli (n-2)*180 astetta. Yksi kulma on siten suuruudeltaan (n-2)*180/n astetta. Viisikulmion yksi kulma on siis 3*180/5=108 astetta, kuusikulmion yksi kulma on 4*180/6=120 astetta, ja seitsenkulmion yksi kulma on 5*180/7=900/7 astetta. Näiden kolmen kulman summa yhdessä kysytyn kulman kanssa tekee luonnollisesti 360 astetta, joten kysytty kulma on 360-108-120-900/7=24/7 astetta.
SUDOKU
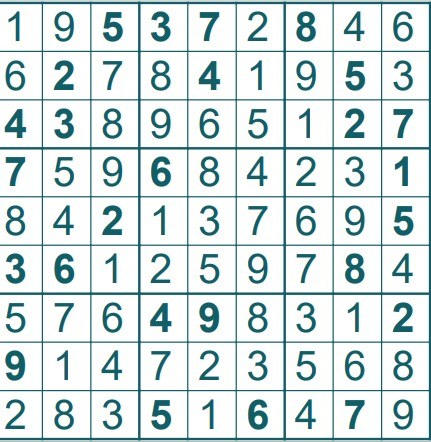
TEK 4/2021 -lehdessä julkaistujen Pulmien ja Sudokun ratkaisut:
PULMA 1.
Ongelma.
Mikä onkaan oheisen seitsensakaraisen tähdykän seitsemän sakaroiden kärjissä sijaitsevan kulman summa?

Ratkaisu.
Nimetkäämme kärjet A, B, C, D, E, F ja G, kuten oheisessa kuvassa, ja nimetkäämme vastaavat kulmat a, b, c, d, e, f ja g, ilmeisellä tavalla.

Tarkastelkaamme suoraa AB. Kun kierrämme sitä pisteen A ympäri kulman a verran, siitä tulee suora AC. Kun kierrämme suoraa uudelleen pisteen C ympäri kulman c verran, siitä tulee suora CD. Jatkamalla samaan tapaan saamme kaikkiaan suorat AB, AC, CD, DE, EF, FG, GB ja BA, missä suoraa on kierretty vastaavasti kulmien a, c, d, e, f, g ja b verran, eli yhteensä kysytyn kulmien summan verran. Toisaalta, suora AB on kääntynyt matkan varrella 180 astetta, joten kysytyn kulmien summan on oltava 180 astetta.
Ongelma.
Elsalla on uusi taskukello. Valitettavasti se vahingoittui kuljetuksessa niin, että kun kello väittää yhden minuutin kuluneen, vain 55 sekuntia on kulunut. Elsa alkaa keittämään pastaa kun kello uskoo, että on keskipäivä, eli 12:00:00, ja pastaa pitää keittää 7 minuuttia --- sekunnin tarkkuudella, sillä kyseessä on hyvin täsmällinen tiede. Mitä aikaa kello näyttää, kun pasta pitää ottaa pois liedeltä?
Ratkaisu.
Pastaa pitää siis keittää 7*60=420 sekuntia. Kun taskukello uskoo x sekuntia kuluneen, tosiasiassa vain 55*x/60 sekuntia on kulunut. Siten 420 sekuntia on kulunut, kun kello uskoo 60*420/55 sekuntia kuluneen. Koska 60*420/55=458+2/11, pasta on valmista (2/11 sekunnin tarkkuudella) kun kello uskoo 458=60*7+38 sekuntia kuluneen, eli kun se näyttää aikaa 12:07:38.
Ongelma.
Pallon muotoisen laatikon tilavuus on
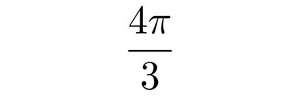
, ja se sisältää kaksi palloa, joiden säteiden a ja b summa on vähintään 1, ja joille a:b=2:3. Kuinka paljon laatikon tilavuudesta on käyttämättä?
Ratkaisu. Koska laatikon tilavuus on 4*pi/3=4*pi*1^3/3, on sen säde 1. Koska säteiden a ja b summa ei voi olla isompi kuin laatikon säde, voi olla siis vain a+b=1. Yhtälöistä a+b=1 ja 3a=2b seuraa, että a=2/5 ja b=3/5. Siten kysytty käyttämätön tilavuus on
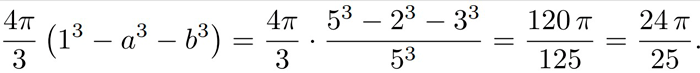
Ongelma.
Pseudodifferentiaalioperaattoritehtaan talousosastolla työskentelee 2021 sihteeriä. Jokainen heistä kuuluu ainakin yhteen komiteaan, ja jokaiseen komiteaan kuuluu täsmälleen kolme sihteeriä. Jos 2020 sihteereistä kuuluu kukin täsmälleen 7 komiteaan, niin kuinka moneen komiteaan on 2021. sihteerin vähintään kuuluttava?
Ratkaisu.
Kuulukoon 2021. sihteeri C komiteaan, ja olkoon talousosastolla kaikkiaan M komiteaa. Yhteensä komiteoiden jäsenten lukumäärien summa on 3M. Toisaalta, tämä on summa niiden komiteoiden määrästä joihin kukin sihteeri kuuluu, missä summa otetaan kaikkien sihteerien yli, joten yhtä suuri kuin 2020*7+C. Koska tämän jälkimmäisen luvun täytyy olla jaollinen kolmella, ja koska luvun 2020*7 jakojäännös kolmella jaettaessa sattuu olemaan 1, täytyy luvun C olla vähintään 2. Toisaalta, osoittautuu, että 2 on mahdollinen luvun C arvo. Voisimme vaikkapa asettaa ensimmäiset 3 sihteeriä samoihin 7 komiteaan, seuraavat kolme sihteeriä joihinkin 7 muuhun samaan komiteaan, ja niin edelleen, ja laittaa 2014., 2015. ja 2016. sihteeri jälleen seitsemään samaan komiteaan. Lopuksi, jäljellä olevat viisi sihteeriä voi asettaa 10 komiteaan vaikkapa näin:

SUDOKU

TEK 3/2021 -lehdessä julkaistujen Pulmien ja Sudokun ratkaisut:
PULMA 1
Ongelma.
Kuvassa on kolme neliötä, joiden sivunpituudet ovat 1, 2 ja 3. Määritä mustan alueen ala.
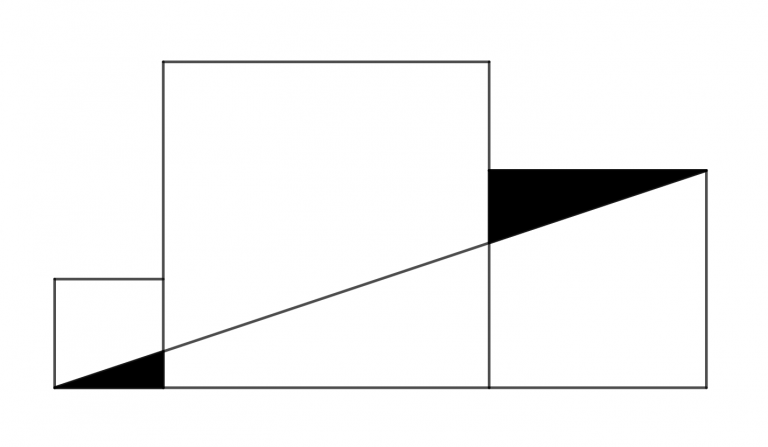
Ratkaisu. Mustat alueet ovat yhdenmuotoisia, sivujen pituuksien mittakaava 2:1. Määritetään pienemmän kolmion korkeus. Se on sama kuin oikeanpuolimmaisen neliön korkeuden suhde koko kuvion pohjaan, eli1/3. Pienemmän mustan kolmion ala on siis 1/6 ja suuremman 4/6, joten yhteensä 5/6.
PULMA 2
Ongelma. Matti ajattelee reaalilukua x, jolle pätee 1<x<2. Voimme pyytää häntä yhden kerran kertomaan jonkin määrän luvun x eniten merkitseviä numeroita. Kuinka monta eniten merkitsevää numeroa meidän on pyydettävä häneltä, jotta voisimme varmasti määrittää vastauksen perusteella luvun x kuution kolme ensimmäistä numeroa?
Ratkaisu. Osoittautuu, että kaikki numerot tarvitaan! Jos nimittäin x on vaikkapa niin lähellä luvun 3 kuutiojuurta, että ensimmäiset 2021 numeroa ovat samat, niin emme vielä pysty sanomaan näiden perusteella, onko x^3<3 vai ei, joten emme pysty määrittämään edes kuution x^3 ensimmäistä numeroa. Ja jos x^3 on tarkalleen 3, niin silloin emme pysty millään äärellisellä määrällä luvun x eniten merkitseviä numeroita päättämään, onko luvun x^3 eniten merkitsevä numero 2 vai 3.
PULMA 3.
Ongelma.
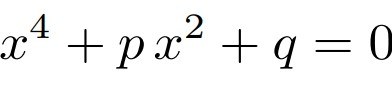
Millä reaalilukupareilla (p,q) on se ominaisuus, että yhtälöllä on neljä reaalijuurta, jotka ovat jonkin aritmeettisen jonon peräkkäisiä jäseniä?
Ratkaisu. Olkoot nollakohdat kasvavassa järjestyksessä a, b, c ja d. Jos x on yhtälön ratkaisu, niin myös -x on. Tästä seuraa, että a=-d ja b=-c. Erityisesti, a ja b ovat epäpositiivisia, ja c ja d epänegatiivisia. Voimme nyt kirjoittaa a=-3e, b=-e, c=e ja d=3e jollekin epänegatiiviselle reaaliluvulle e. Alkuperäisen yhtälön vasemman puolen täytyy tällöin olla
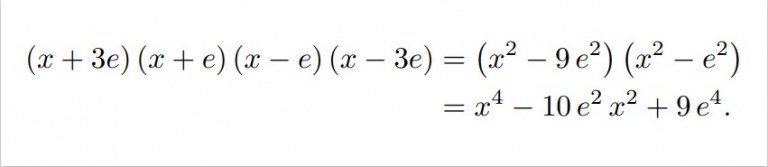
Ja tämä toteutuukin täsmälleen silloin, kun (p,q)=(-10e^2,9e^4).
PULMA 4
Ongelma.
Tarkastellaan kasvavaa positiivisten kokonaislukujen jonoa 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, ..., missä kukin positiivinen kokonaisluku n esiintyy täsmälleen 1+2+...+n kertaa. Mikä onkaan jonon 2021. jäsen?
Ratkaisu.
Olkoon a positiivinen kokonaisluku. Silloin enintään luvun a kokoisten jonon jäsenten lukumäärä on
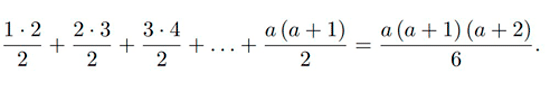
Tässä viimeinen yhtäsuuruus seuraa vaikkapa havainnoista
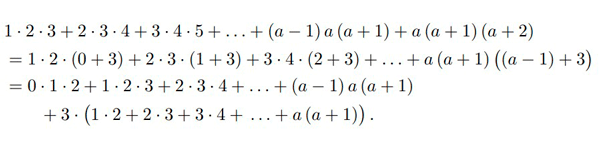
Siten 2021. jäsen jonossa on a+1 jos ja vain jos
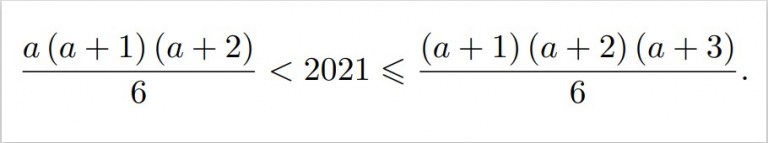
Koska
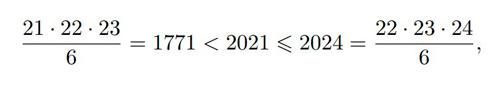
on 2021. jäsenen oltava 22.
SUDOKU.